El Coeficiente de Curtosis analiza el grado de concentración que presentan los valores alrededor de la zona central de la distribución.
Se definen 3 tipos de distribuciones según su grado de curtosis:
Distribución mesocúrtica: presenta un grado de concentración medio alrededor de los valores centrales de la variable (el mismo que presenta una distribución normal).
Distribución leptocúrtica: presenta un elevado grado de concentración alrededor de los valores centrales de la variable.
Distribución platicúrtica: presenta un reducido grado de concentración alrededor de los valores centrales de la variable.
El Coeficiente de Curtosis viene definido por la siguiente fórmula:
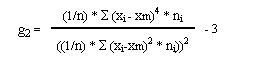
Los resultados pueden ser los siguientes:
g2 = 0 (distribución mesocúrtica).g2 > 0 (distribución leptocúrtica).
g2 <>.
Ejemplo: Vamos a calcular el Coefiente de Curtosis de la serie de datos referidos a la estatura de un grupo de alumnos (lección 2ª):
| Variable | Frecuencias absolutas | Frecuencias relativas | ||
| (Valor) | Simple | Acumulada | Simple | Acumulada |
| x | x | x | x | x |
| 1,20 | 1 | 1 | 3,3% | 3,3% |
| 1,21 | 4 | 5 | 13,3% | 16,6% |
| 1,22 | 4 | 9 | 13,3% | 30,0% |
| 1,23 | 2 | 11 | 6,6% | 36,6% |
| 1,24 | 1 | 12 | 3,3% | 40,0% |
| 1,25 | 2 | 14 | 6,6% | 46,6% |
| 1,26 | 3 | 17 | 10,0% | 56,6% |
| 1,27 | 3 | 20 | 10,0% | 66,6% |
| 1,28 | 4 | 24 | 13,3% | 80,0% |
| 1,29 | 3 | 27 | 10,0% | 90,0% |
| 1,30 | 3 | 30 | 10,0% | 100,0% |
Recordemos que la media de esta muestra es 1,253
| S((xi - xm)^4)*ni | S((xi - xm)^2)*ni |
| x | x |
| 0,00004967 | 0,03046667 |
Luego:
|
| (1/30) * 0,00004967 |
|
|
| g2 = | ------------------------------------------------- | - 3 | = -1,39 |
|
| ((1/30) * (0,03046667))^2 |
|
|
Por lo tanto, el Coeficiente de Curtosis de esta muestra es -1,39, lo que quiere decir que se trata de una distribución platicúrtica, es decir, con una reducida concentración alrededor de los valores centrales de la distribución.







No hay comentarios:
Publicar un comentario